Cây quyết định là gì? Hướng dẫn xây dựng cây quyết định dự báo thời tiết bằng thuật toán ID3

1. Cây quyết định là gì?

Cây quyết định (có tên tiếng Anh là Decision Tree) là cây phân cấp có cấu trúc. Cây quyết định được sử dụng để xây dựng các mô hình và phân loại các đối tượng dưới dạng cấu trúc cây. Các đối tượng sẽ có thuộc tính thuộc nhiều kiểu dữ liệu như Nominal (định danh), Quantitative (số lượng), Ordinal (thứ tự), Binary (nhị phân).

Một số thuật toán thường được sử dụng trong cây quyết định có thể kể ra là: ID3, C4.5, CART, CHAID và MARS.

2. Thuật toán ID3 là gì?

ID3 là từ viết tắt của cụm từ Iterative Dichotomiser 3. ID3 là một thuật toán phân loại theo cách tiếp cận tham lam bằng cách chọn thuộc tính tốt nhất nhằm mang lại Information Gain (IG - lợi ích của thông tin) tối đa hoặc Entropy tối thiểu (entropy dùng để chỉ trạng thái ngẫu nhiên hoặc không có trật tự).

Thuật toán ID3 thực hiện các bước lần lượt như sau:

• Tính entropy của tập dữ liệu
• Đối với mỗi thuộc tính/ tính năng: ID3 sẽ tính entropy cho tất cả giá trị phân loại và mức IG của tính năng đó
• Tìm kiếm tính năng để có được IG tối đa
• Lặp lại các bước thực hiện cho đến khi đạt được cây mong muốn

3. Xây dựng cây quyết định dự báo thời tiết bằng thuật toán ID3

Để các bạn có thể hiểu rõ hơn cây quyết định là gì, chúng ta hãy cùng làm một ví dụ về việc xây dựng mô hình cây quyết định dự báo thời tiết. 

Chúng ta có bảng dữ liệu như sau:

Tập dữ liệu trên thuộc các lớp nhị phân: Yes/ No (có hoặc không), trong đó 9 dữ liệu là “Yes” và 5 dữ liệu là “No”.

Chúng ta sẽ có entropy đầy đủ của tập dữ liệu là:

H(S) = - p(yes) * log2(p(yes)) - p(no) * log2(p(no))

     = - (9/14) * log2(9/14) - (5/14) * log2(5/14)

     = - (-0.41) - (-0.53)
    = 0.94

Với mỗi thuộc tính của tập dữ liệu, bạn hãy làm theo các bước sau:

• Thuộc tính Outlook

Categorical values - sunny, overcast and rain

H(Outlook=sunny) = -(2/5)*log(2/5)-(3/5)*log(3/5) =0.971

H(Outlook=rain) = -(3/5)*log(3/5)-(2/5)*log(2/5) =0.971

H(Outlook=overcast) = -(4/4)*log(4/4)-0 = 0

Average Entropy Information for Outlook - 

I(Outlook) = p(sunny) * H(Outlook=sunny) + p(rain) * H(Outlook=rain) + p(overcast) * H(Outlook=overcast)

= (5/14)*0.971 + (5/14)*0.971 + (4/14)*0

= 0.693

Information Gain = H(S) - I(Outlook)

                 = 0.94 - 0.693
      = 0.247

• Thuộc tính Temperature

Categorical values - hot, mild, cool

H(Temperature=hot) = -(2/4)*log(2/4)-(2/4)*log(2/4) = 1

H(Temperature=cool) = -(3/4)*log(3/4)-(1/4)*log(1/4) = 0.811

H(Temperature=mild) = -(4/6)*log(4/6)-(2/6)*log(2/6) = 0.9179

Average Entropy Information for Temperature - 

I(Temperature) = p(hot)*H(Temperature=hot) + p(mild)*H(Temperature=mild) + p(cool)*H(Temperature=cool)

= (4/14)*1 + (6/14)*0.9179 + (4/14)*0.811

= 0.9108

Information Gain = H(S) - I(Temperature)

                 = 0.94 - 0.9108

      = 0.0292

• Thuộc tính Humidity

Categorical values - high, normal

H(Humidity=high) = -(3/7)*log(3/7)-(4/7)*log(4/7) = 0.983

H(Humidity=normal) = -(6/7)*log(6/7)-(1/7)*log(1/7) = 0.591

Average Entropy Information for Humidity - 

I(Humidity) = p(high)*H(Humidity=high) + p(normal)*H(Humidity=normal)

= (7/14)*0.983 + (7/14)*0.591 

= 0.787

Information Gain = H(S) - I(Humidity)

                 = 0.94 - 0.787

      = 0.153

• Thuộc tính Wind

Categorical values - weak, strong

H(Wind=weak) = -(6/8)*log(6/8)-(2/8)*log(2/8) = 0.811

H(Wind=strong) = -(3/6)*log(3/6)-(3/6)*log(3/6) = 1

Average Entropy Information for Wind - 

I(Wind) = p(weak)*H(Wind=weak) + p(strong)*H(Wind=strong)

= (8/14)*0.811 + (6/14)*1 

= 0.892

Information Gain = H(S) - I(Wind)

                 = 0.94 - 0.892

      = 0.048

Đến đây, thuộc tính có được thông tin tối đa là Outlook. Vì vậy, cây quyết định ID3 được xây dựng như sau:

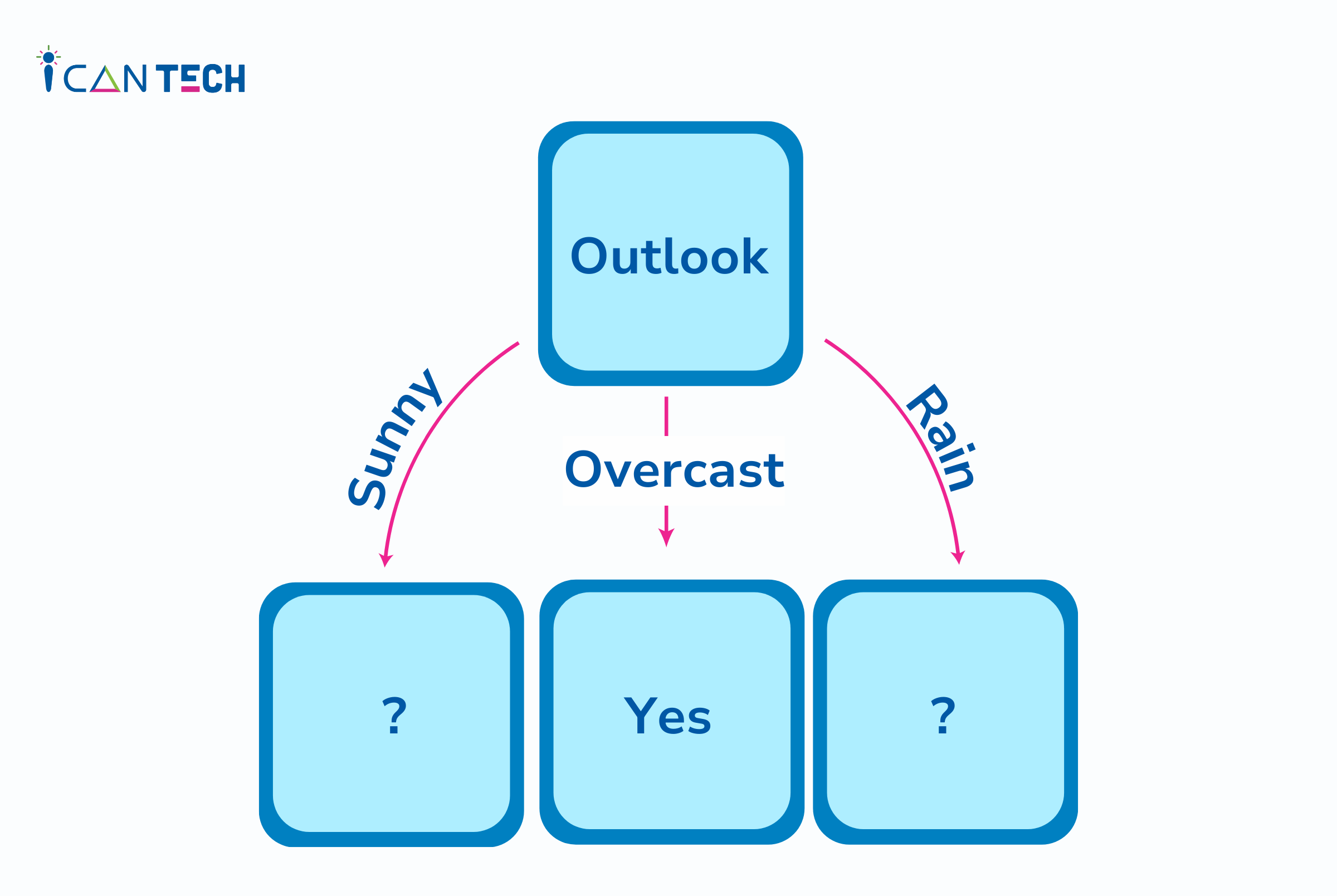
Bước tiếp theo, bạn sẽ làm lại các bước tương tự cho dữ liệu của các hàng bao gồm giá trị Outlook là Sunny và Rain. Bắt đầu với việc tìm thuộc tính tốt nhất để phân tách dữ liệu với Outlook=Sunny values{ Dataset rows = [1, 2, 8, 9, 11]}.

Complete entropy of Sunny is -

H(S) = - p(yes) * log2(p(yes)) - p(no) * log2(p(no))

     = - (2/5) * log2(2/5) - (3/5) * log2(3/5)

     = 0.971

• Thuộc tính Temperature

Categorical values - hot, mild, cool

H(Sunny, Temperature=hot) = -0-(2/2)*log(2/2) = 0

H(Sunny, Temperature=cool) = -(1)*log(1)- 0 = 0

H(Sunny, Temperature=mild) = -(1/2)*log(1/2)-(1/2)*log(1/2) = 1

Average Entropy Information for Temperature - 

I(Sunny, Temperature) = p(Sunny, hot)*H(Sunny, Temperature=hot) + p(Sunny, mild)*H(Sunny, Temperature=mild) + p(Sunny, cool)*H(Sunny, Temperature=cool)

= (2/5)*0 + (1/5)*0 + (2/5)*1

= 0.4

Information Gain = H(Sunny) - I(Sunny, Temperature)

                 = 0.971 - 0.4

      = 0.571

• Thuộc tính Humidity

Categorical values - high, normal

H(Sunny, Humidity=high) = - 0 - (3/3)*log(3/3) = 0

H(Sunny, Humidity=normal) = -(2/2)*log(2/2)-0 = 0

Average Entropy Information for Humidity - 

I(Sunny, Humidity) = p(Sunny, high)*H(Sunny, Humidity=high) + p(Sunny, normal)*H(Sunny, Humidity=normal)

= (3/5)*0 + (2/5)*0 

= 0

Information Gain = H(Sunny) - I(Sunny, Humidity)

                 = 0.971 - 0

                 = 0.971

• Thuộc tính Wind

Categorical values - weak, strong
H(Sunny, Wind=weak) = -(1/3)*log(1/3)-(2/3)*log(2/3) = 0.918
H(Sunny, Wind=strong) = -(1/2)*log(1/2)-(1/2)*log(1/2) = 1

Average Entropy Information for Wind - 
I(Sunny, Wind) = p(Sunny, weak)*H(Sunny, Wind=weak) + p(Sunny, strong)*H(Sunny, Wind=strong)
= (3/5)*0.918 + (2/5)*1 
= 0.9508

Information Gain = H(Sunny) - I(Sunny, Wind)
      = 0.971 - 0.9508
      = 0.0202

Mô hình cây quyết định lúc này như sau:
 

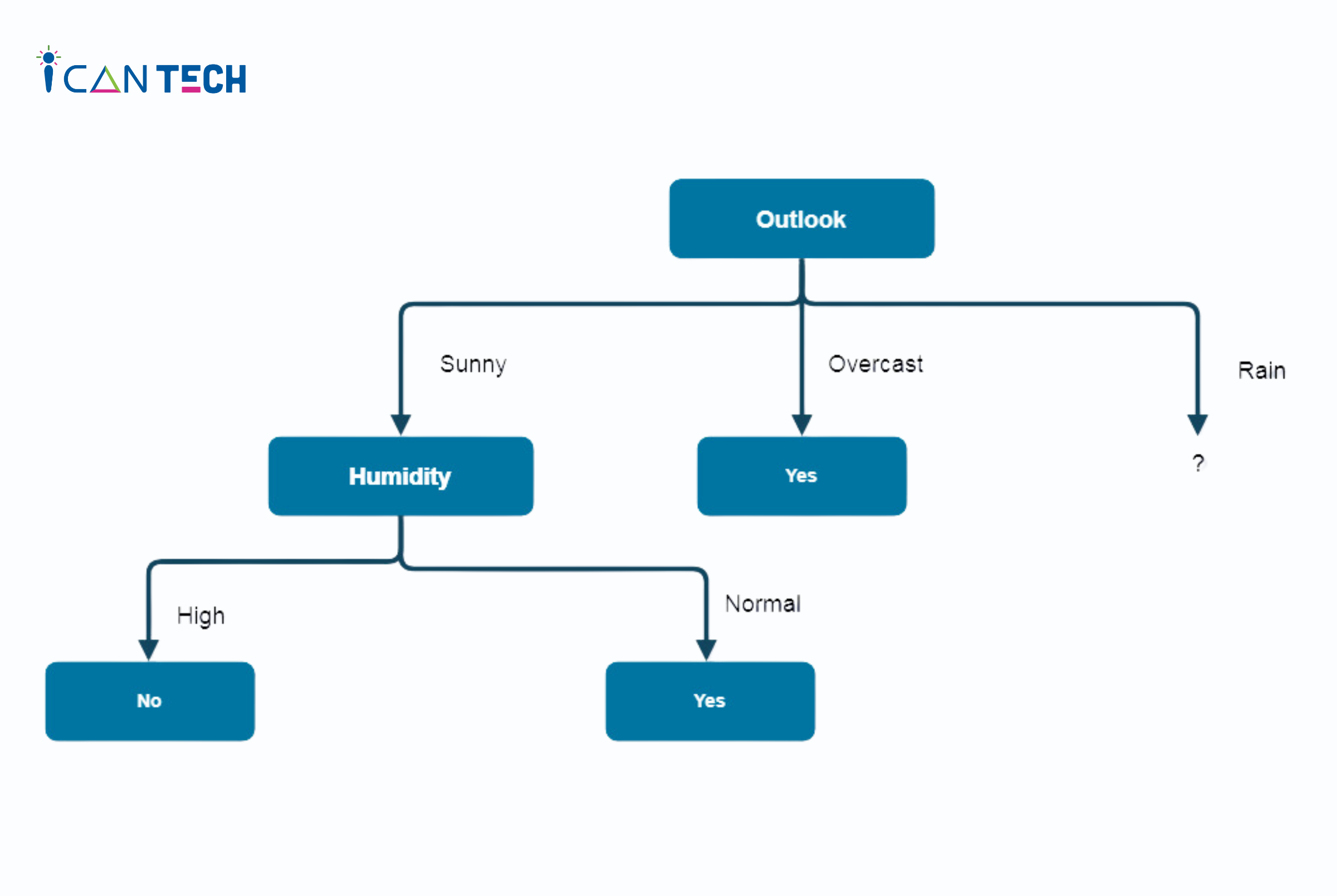
Tiếp theo, chúng ta sẽ đi tìm thuộc tính tốt nhất để phân tách dữ liệu với Outlook=Sunny values{ Dataset rows = [4, 5, 6, 10, 14]}.

Complete entropy of Rain is -
H(S) = - p(yes) * log2(p(yes)) - p(no) * log2(p(no))
        = - (3/5) * log(3/5) - (2/5) * log(2/5) 
        = 0.971
 

• Thuộc tính Temperature

Categorical values - mild, cool
H(Rain, Temperature=cool) = -(1/2)*log(1/2)- (1/2)*log(1/2) = 1
H(Rain, Temperature=mild) = -(2/3)*log(2/3)-(1/3)*log(1/3) = 0.918

Average Entropy Information for Temperature - 
I(Rain, Temperature) = p(Rain, mild)*H(Rain, Temperature=mild) + p(Rain, cool)*H(Rain, Temperature=cool)
= (2/5)*1 + (3/5)*0.918
= 0.9508

Information Gain = H(Rain) - I(Rain, Temperature)
      = 0.971 - 0.9508
      = 0.0202

• Thuộc tính Wind

Categorical values - weak, strong
H(Wind=weak) = -(3/3)*log(3/3)-0 = 0
H(Wind=strong) = 0-(2/2)*log(2/2) = 0

Average Entropy Information for Wind - 
I(Wind) = p(Rain, weak)*H(Rain, Wind=weak) + p(Rain, strong)*H(Rain, Wind=strong)
= (3/5)*0 + (2/5)*0 
= 0

Information Gain = H(Rain) - I(Rain, Wind)
      = 0.971 - 0
      = 0.971

Cuối cùng, chúng ta có được cây quyết định được xây dựng như sau:
 

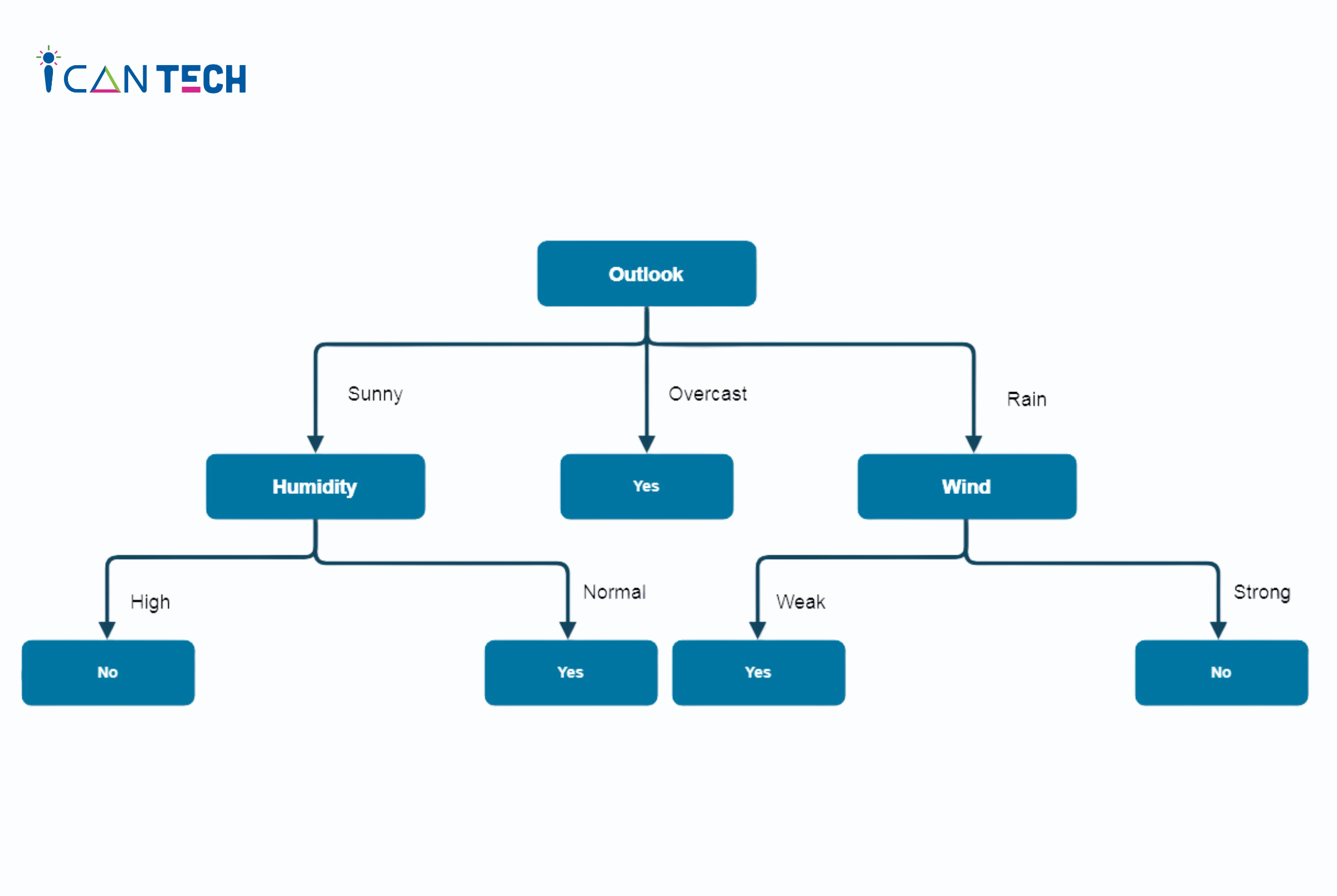
4. Lời Kết

Trước khi bắt tay vào xây dựng cây quyết định, bạn cần phải nắm chắc kiến thức cây quyết định là gì và cách sử dụng thuật toán ID3. Mong rằng với 1 ví dụ xây dựng mô hình cây quyết định ở bài biết, bạn đã có thêm kinh nghiệm để áp dụng vào thực tế. Chúc bạn thành công!

Nếu bạn đang quan tâm đến học lập trình thì hãy tham khảo ngay các khóa học lập trình tại ICANTECH nhé

• Khóa học lập trình Web
• Khóa học lập trình Python

Nguồn ảnh: ICANTECH.