Tìm ước chung lớn nhất Python

1. Định nghĩa ước chung lớn nhất

Ước chung lớn nhất (UCLN) của 2 số nguyên dương a và b là một số k lớn nhất, sao cho a và b đều chia hết cho k.

Bội số chung nhỏ nhất (BSCNN) của 2 số nguyên dương a và b là một số h nhỏ nhất, sao cho h chia hết cho cả a và b.

Hình minh họa:

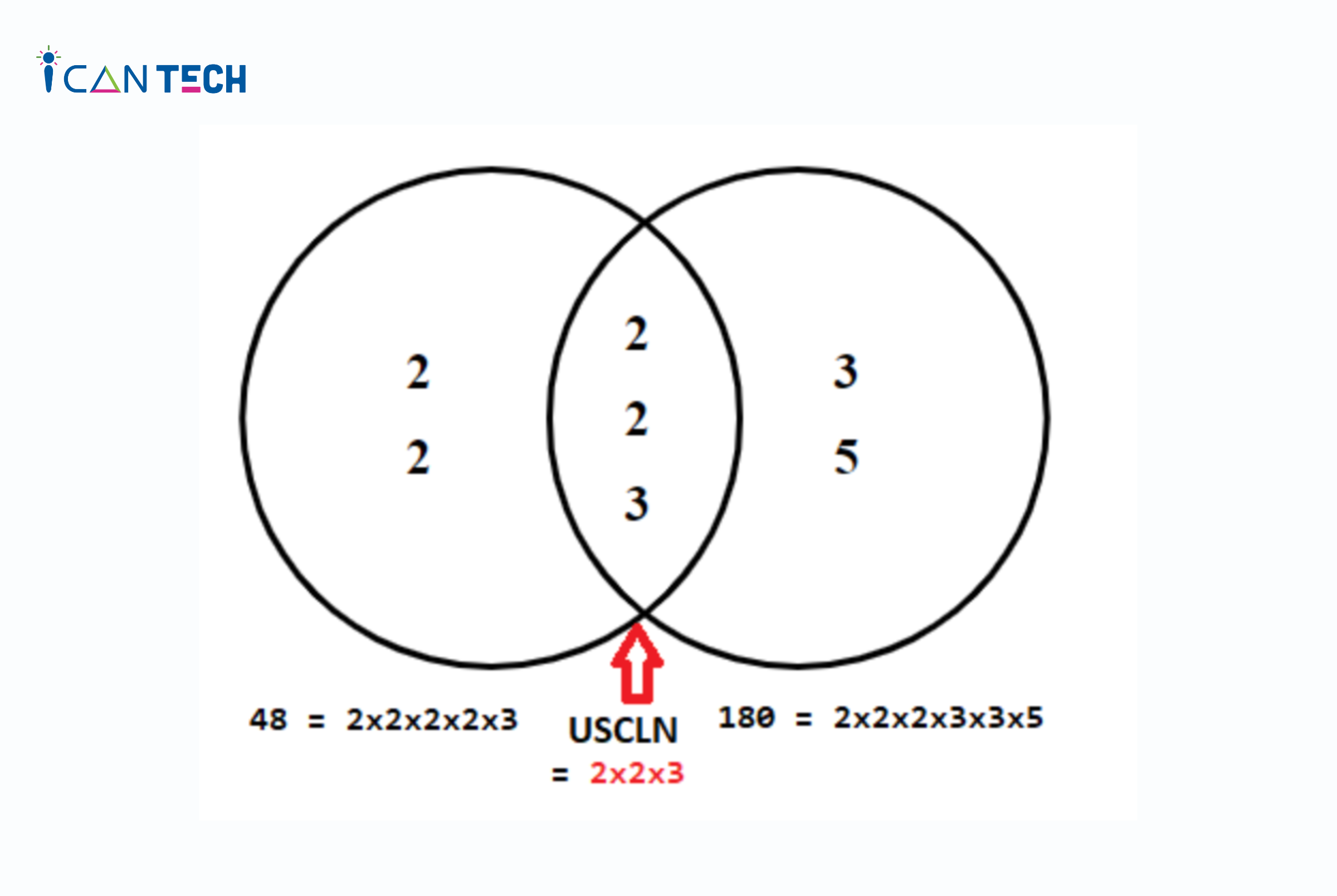
2. Bài toán tìm ước chung lớn nhất trong Python

Được hiểu bài toán này sẽ yêu cầu chúng ta viết chương trình nhận 2 số nguyên từ bàn phím và tìm ước chung lớn nhất của 2 số nguyên đó.

Ý tưởng:

• Cách 1: Sử dụng thuật toán Euclid
• Cách 2: Sử dụng hàm tìm ước chung lớn nhất trong Python

2.1. Sử dụng thuật toán Euclid để tìm ước chung lớn nhất

Mô tả ý tưởng của thuật toán:

Ta sẽ dùng phép chia dư liên tục cho đến khi tìm được ước chung lớn nhất Python 

Ví dụ:

Tính ước số chung lớn nhất của 35 và 28.

Trước hết lấy 35 (số lớn hơn trong 2 số) chia cho 28:

35 = 28*1 + 7 (28 & 7 sẽ được dùng cho vòng lặp kế)

Nhận xét: Với bất kỳ số nguyên nào được chia hết bởi 35 và 28 cũng sẽ chia hết bởi 35 - 28*1 = 14. Tương tự, số chia hết bởi 28 và 7 cũng chia hết bởi 28*1 +7 = 35. Do đó, ƯCLN(35,28) = ƯSCLN(28,7). 

Từ đây bài toán trở thành tìm ƯCLN(28,7). Tiếp tục lặp lại quy trình cho đến khi phép chia không còn số dư như sau:

28 = 7*4 + 0 (không còn dư)

Cuối cùng ta có: 7 = UCLN(7,0) = UCLN(28,7) = UCLN(35,28).

Từ ý tưởng trên ta cũng có thể suy ra ý tưởng tìm BCNN như sau:

BCNN của a, b được tính dựa trên UCLN của 2 số đó theo công thức:

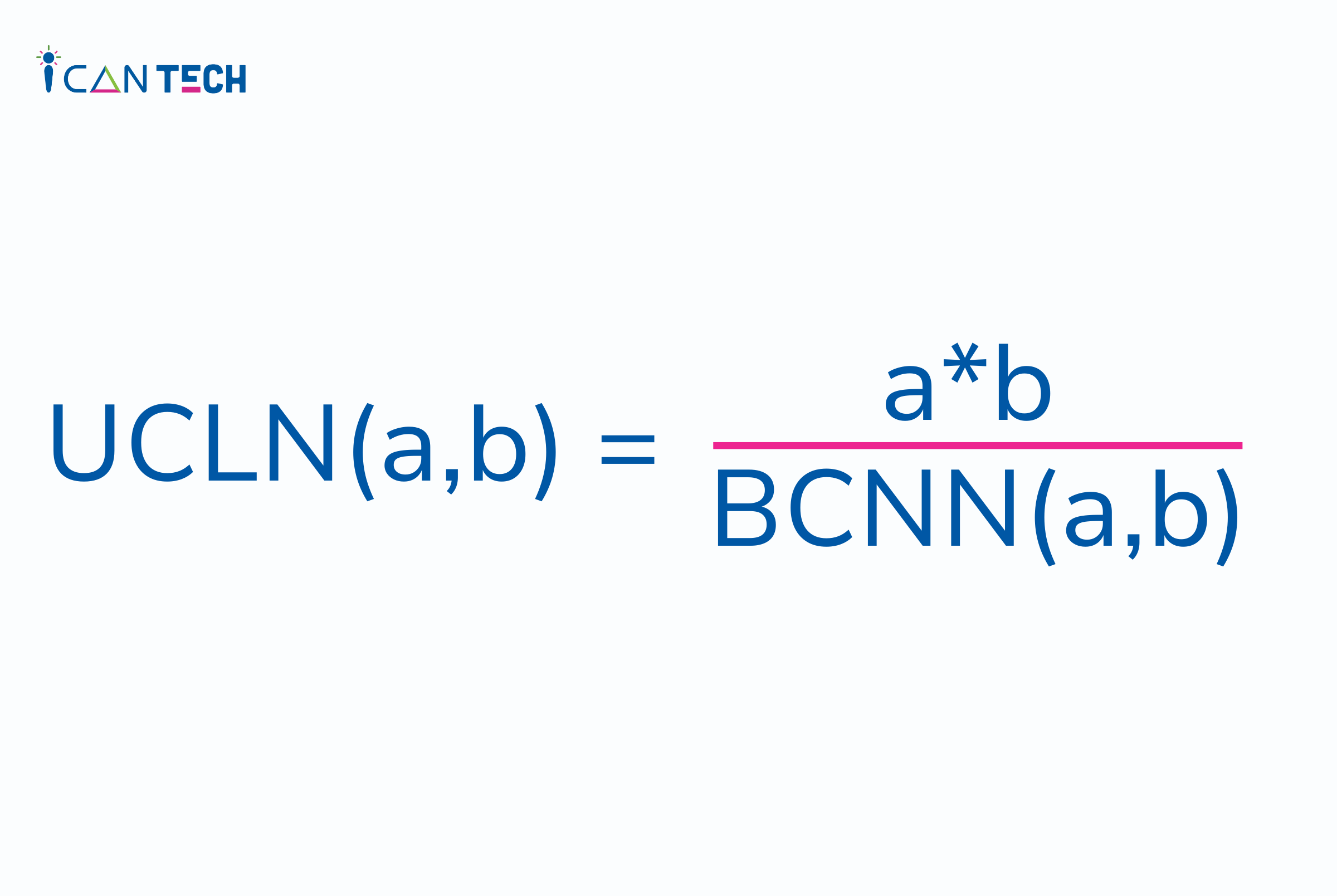
Cài đặt thuật toán Euclid tìm ước chung lớn nhất bằng chương trình Python:

#Khởi tạo hàm

def UCLN(a, b):

#Kiểm tra nếu bằng 0 thì a là ƯCLN

if (b == 0):

return a

#Nếu b khác 0 thì tìm UCLN của b và số dư của a cho b

else:

return UCLN(b, a % b)

print(UCLN(35, 28))

Kết quả: 7

Nhận xét thuật toán Euclid cho bài toán tìm ước chung lớn nhất:

Ưu điểm: Đơn giản, dễ hiểu

Nhược điểm: Tốn nhiều thời gian tính toán do phải thực hiện chia nhiều lần 

2.2. Sử dụng hàm tìm ước chung lớn nhất trong Python

Python cung cấp hàm gcd() trong thư viện math để hỗ trợ việc tìm UCLN của 2 số nguyên.

Ví dụ:

import math

a = 35

b = 28

print(math.gcd(a, b))

Kết quả:

7

Hàm này giúp tính toán nhanh hơn so với việc tự code theo ý tưởng của thuật toán Euclid bằng Python. 

Do đó, chúng ta nên sử dụng cách này để tìm ƯCLN của 2 số nguyên.

3. Ứng dụng bài toán tìm ước chung lớn nhất Python

3.1. Tìm ước chung lớn nhất của nhiều số nguyên

Thay vì tìm ƯCLN của 2 số nguyên thì bài toán mở rộng sẽ tìm ước chung lớn nhất của lớn hơn 2 số nguyên.

Ý tưởng: Tách các số thành các cặp số và sử dụng vòng lặp for để tìm UCLN của từng cặp.

Ví dụ:

import math

def UCLN(numbers):

result = numbers[0]

#Lần lượt duyệt từng cặp số

for i in range(1, len(numbers)):

result = math.gcd(result, numbers[i])

return result

print(UCLN([10, 90, 25]))

Kết quả:

5

3.2. Tìm hợp số chung của 2 số nguyên

Hợp số chung của 2 số nguyên a và b chính là tích giữa ƯCLN và BCNN của chúng.

Ý tưởng: Sử dụng hàm gcd() để tìm ƯCLN sau đó áp dụng công thức tìm BCNN. Đưa ra kết quả là tích của 2 số.

import math

def hop_so(a, b):

return a * b // math.gcd(a, b)

a, b = 8, 9

print(math.gcd(a, b) * hop_so(a, b))

Kết quả: 189

4. Lời Kết

Như vậy, bài viết đã chỉ ra các cách giải quyết bài toán tìm ước chung lớn nhất Python của 2 số nguyên. Việc vận dụng bài toán để xử lý các kiến thức trong thực tế là vô cùng phong phú vì vậy các bạn hãy ứng dụng các kiến thức ở trên để có thể sử dụng thành thạo và tối ưu chương trình của mình. Chúc các bạn thành công!

Nếu bạn đang quan tâm đến học lập trình online thì hãy tham khảo ngay các khóa học lập trình tại ICANTECH nhé

Nguồn ảnh: ICANTECH.